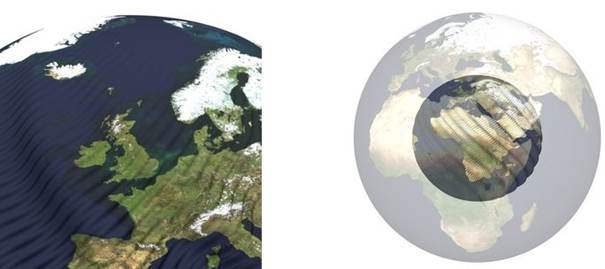
Première image d’une sphère réduite en 3D : faire entrer la surface de la Terre à l'intérieur d'une balle de ping-pong
Dans les années 1950, Nicolas Kuiper et le prix Nobel John Nash ont démontré l’existence d’une vaste classe d’objets mathématiques paradoxaux, tels que des tores plats en 3D, ou de sphères réduites, sans pouvoir toutefois les visualiser. Une équipe de mathématiciens et d’informaticiens du CNRS(1), de l’Univ. Grenoble Alpes(1) et de l’Université Claude Bernard Lyon(1), a réussi à construire et représenter visuellement une sphère réduite, cinq ans après avoir obtenu la première image d’un tore plat en 3D(2).